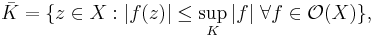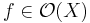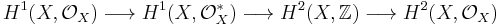Stein manifold

In mathematics, a Stein manifold in the theory of several complex variables and complex manifolds is a complex submanifold of the vector space of n complex dimensions. The name is for Karl Stein.

1 Definition
2 Non-compact Riemann surfaces are Stein
3 Properties and examples of Stein manifolds
4 Notes
5 References

Definition

A complex manifold $X$ of complex dimension $n$ is called a Stein manifold if the following conditions hold:

$X$ is holomorphically convex, i.e. for every compact subset $K \subset X$ , the so-called holomorphic convex hull,

$\bar K = \{z \in X: |f(z)| \leq \sup_K |f| \ \forall f \in \mathcal O(X) \},$

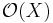is again a compact subset of $X$ . Here $\mathcal O(X)$ denotes the ring of holomorphic functions on $X$ .

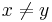$X$ is holomorphically separable, i.e. if $x \neq y$ are two points in $X$ , then there is a holomorphic function

$f \in \mathcal O(X)$

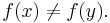
such that $f(x) \neq f(y).$

Non-compact Riemann surfaces are Stein

Let X be a connected non-compact Riemann surface. A deep theorem of Behnke and Stein (1948) asserts that X is a Stein manifold.

Another result, attributed to Grauert and Röhrl (1956), states moreover that every holomorphic vector bundle on X is trivial.

In particular, every line bundle is trivial, so 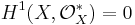$H^1(X, \mathcal O_X^*) =0$ . The exponential sheaf sequence leads to the following exact sequence:

$H^1(X, \mathcal O_X) \longrightarrow H^1(X, \mathcal O_X^*) \longrightarrow H^2(X, \mathbb Z) \longrightarrow H^2(X, \mathcal O_X)$

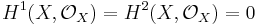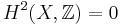Now Cartan's theorem B shows that $H^1(X, \mathcal O_X)= H^2(X, \mathcal O_X)=0$ , therefore $H^2(X, \mathbb Z)=0$ .

This is related to the solution of the Cousin problems, and more precisely to the second Cousin problem.

Properties and examples of Stein manifolds

The standard complex space 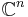$\mathbb C^n$ is a Stein manifold.
It can be shown quite easily that every closed complex submanifold of a Stein manifold is a Stein manifold, too.
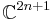The embedding theorem for Stein manifolds states the following: Every Stein manifold $X$ of complex dimension $n$ can be embedded into $\mathbb C^{2 n%2B1}$ by a biholomorphic proper map.

These facts imply that a Stein manifold is a closed complex submanifold of complex space, whose complex structure is that of the ambient space (because the embedding is biholomorphic).

In one complex dimension the Stein condition can be simplified: a connected Riemann surface is a Stein manifold if and only if it is not compact. This can be proved using a version of the Runge theorem for Riemann surfaces, due to Behnke and Stein.
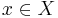Every Stein manifold $X$ is holomorphically spreadable, i.e. for every point $x \in X$ , there are $n$ holomorphic functions defined on all of $X$ which form a local coordinate system when restricted to some open neighborhood of $x$ .
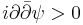Being a Stein manifold is equivalent to being a (complex) strongly pseudoconvex manifold. The latter means that it has a strongly pseudoconvex (or plurisubharmonic) exhaustive function, i.e. a smooth real function $\psi$ on $X$ (which can be assumed to be a Morse function) with $i \partial \bar \partial \psi >0$ , such that the subsets 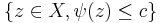$\{z \in X, \psi (z)\leq c \}$ are compact in $X$ for every real number $c$ . This is a solution to the so-called Levi problem,^[1] named after E. E. Levi (1911). The function $\psi$ invites a generalization of Stein manifold to the idea of a corresponding class of compact complex manifolds with boundary called Stein domains. 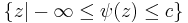A Stein domain is the preimage $\{z|-\infty\leq\psi(z)\leq c\}$ . Some authors call such manifolds therefore strictly pseudoconvex manifolds.
Related to the previous item, another equivalent and more topological definition in complex dimension 2 is the following: a Stein surface is a complex surface X with a real-valued Morse function f on X such that, away from the critical points of f, the field of complex tangencies to the preimage X_c = f⁻¹(c) is a contact structure that induces an orientation on X_c agreeing with the usual orientation as the boundary of f⁻¹(−∞,c). That is, f⁻¹(−∞,c) is a Stein filling of X_c.

Numerous further characterizations of such manifolds exist, in particular capturing the property of their having "many" holomorphic functions taking values in the complex numbers. See for example Cartan's theorems A and B, relating to sheaf cohomology. The initial impetus was to have a description of the properties of the domain of definition of the (maximal) analytic continuation of an analytic function.

In the GAGA set of analogies, Stein manifolds correspond to affine varieties.

Stein manifolds are in some sense dual to the elliptic manifolds in complex analysis which admit "many" holomorphic functions from the complex numbers into themselves. It is known that a Stein manifold is elliptic if and only if it is fibrant in the sense of so-called "holomorphic homotopy theory".

Notes

^ PlanetMath: solution of the Levi problem

References

Forster, Otto (1981), Lectures on Riemann surfaces, Graduate Text in Mathematics, 81, New-York: Springer Verlag, ISBN 0-387-90617-7 (including a proof of Behnke-Stein and Grauert-Röhrl theorems)
Hörmander, Lars (1990), An introduction to complex analysis in several variables, North-Holland Mathematical Library, 7, Amsterdam: North-Holland Publishing Co., ISBN 978-0-444-88446-6, MR 1045639 (including a proof of the embedding theorem)
Gompf, Robert E. (1998), "Handlebody construction of Stein surfaces", Annals of Mathematics. Second Series (The Annals of Mathematics, Vol. 148, No. 2) 148 (2): 619–693, doi:10.2307/121005, ISSN 0003-486X, JSTOR 121005, MR 1668563 (definitions and constructions of Stein domains and manifolds in dimension 4)